Ludwig Peetz Reconstruction of the Welte-Mignon T100 recording system technology p. 5
"Light touch: small line on then paper; hard key stroke, wider line. Slow key depression: gradual
widening of the line hard key stroke, rapid expansion of the line.
Then some smart technicians at the Welte factory could interpret the loudness by not only the width of
of the line but also the rate over of the line expanding."
Only with both parameters it is able to detect correctly, what I did with the piano: playing a pp-note and
then pressing the key with maximum force as it would be a ff-note. The relevant position, where the
hammer leaves the thrower to the string, is corresponding to a given position e.g. to a line width of 0,5
mm. At this point you will detect a small expanding rate, so you can verify, that it was a soft tone
played, in spite of the fact that the slope then increases and the line width increases up to a high value
of e.g. 3 mm, which corresponds to a very high force. Thus, only the combination of the two
parameters position and velocity makes you sure what really happened!
5. Description of the Welte-Mignon Recording Process
Richard Simonton jr. cited his father from "In Search of Recorded treasures The Welte Master Roll
adventure of 1948" /3/:
"There was a standard Steinway grand piano, equipped with a trough running the length of the
keyboard and immediately under it. In this trough, there was a pool of mercury, and when the key was
depressed, a carbon rod attached to the bottom of the key engaged the mercury and caused an
electrical contact to be made. The resistance of this contact varied with the pressure exerted on the
carbon rod so that actually , depending upon the blow with which the key was struck, there was a
corresponding change in the electrical resistance of the contact made.
All of the keys were connected by wires to the recording machine with was usually some feet away
from the controlling piano. This machine had within it the conventional rolls of paper which were
entirely blank and without perforations, but were ruled their entire length with over 100 fine lines, each
corresponding to the center line of its control mechanism. Above the point at which the impression
actually took place on the paper was a series of small rubber rollers of a composition similar to the type
used in a printing press, and these rollers were inked with an ink similar to that used in the printing
industry."
There is another description by Ben Hall used with the permission of Mr. Richard C. Simonton /4/:
"The recording unit, connected to a Feurich grand piano in the Welte music hall, contained a roll of
specially-aged, thin paper, marked off into 100 parallel lines. Poised over each line was a little wheel of
extremely soft rubber, with pointed edges. Each wheel was in contact with an ink supply, and in this
much of the process is resembled a small offset printing press. Under the keyboard of the recording
piano was a trough filled with mercury; attached to the underside of each key was slim rod of carbon.
As the key was depressed, the rod dipped into the mercury and an electrical contact was established
between it and an electromagnet connected to the corresponding inked roller in the recording machine.
The harder the artist hit the key of the piano, the deeper the carbon rod would plunge into the mercury,
and the stronger the current between the rod and the electromagnet would be. The harder the inked
rubber wheel was pressed against the moving paper roll, the wider the mark it printed on the paper.
The pianist's pedaling and speed of attack was captured in the same way."
Both descriptions of the Welte-Mignon registration unit is very similar to that of Kurt Binninger's
description /5/ of the Philharmonic Organ Registration System at Freiburg (see fig. 5). Kurt Binninger
worked at Welte, Freiburg in the 1930's /6/.
In contrast to the Freiburg system the American organ registration machine (now in the Swiss museum
in Seewen) worked with an indirect electrical-pneumatic lever system. In both organ recording systems
metal disks have been used instead of rubber disks (because there is no need to register dynamics).
Ludwig Peetz Reconstruction of the Welte-Mignon T100 recording system technology p. 6
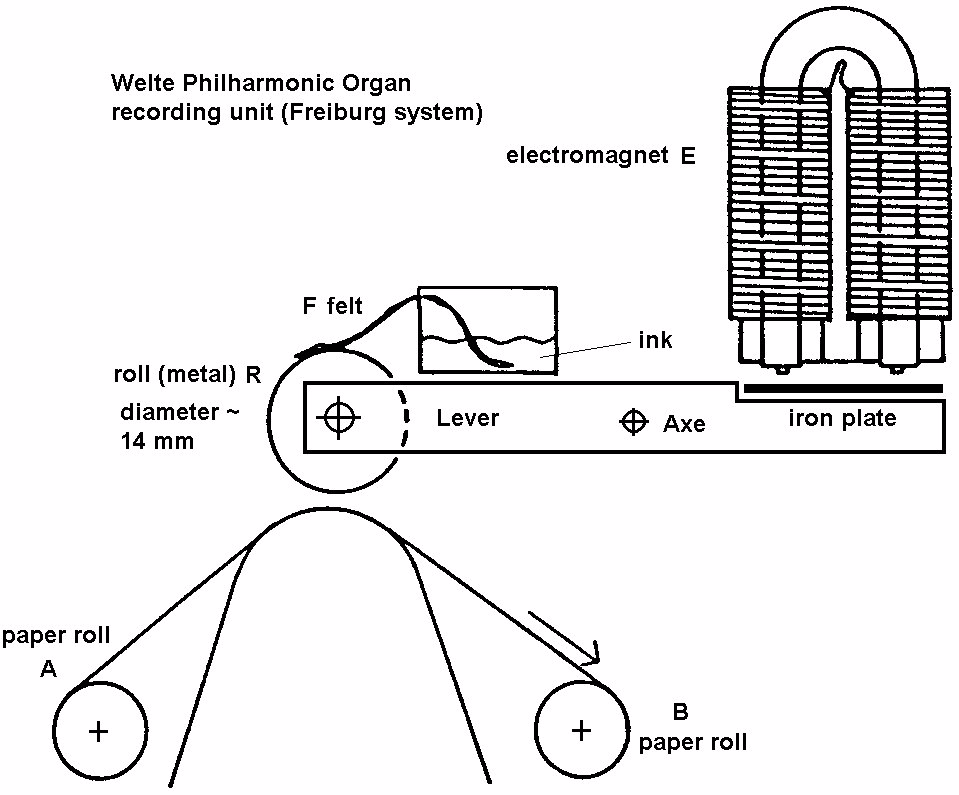
Fig. 5.: The Welte Philharmonic organ recording unit (Freiburg system; according to /5/)
6. Width of Lines printed by Elastic Disks
I investigated the line width / force behaviour of elastic disks with its originally round section and with a
modified sharpened form (by sanding it manually). The disks have outer rings of rubber-like
polyurethane (hardness: ~ shore 80 A) with following properties:
original sharpened
diameter: 50 mm 49 mm
thickness: 6 mm 4 mm
section: half circle triangle with an angle of approx. 75°
Disks sharpened to a lower angle (45°) couldn't be used because of folding problems when pressed
against the paper.
The disks have been mounted in a roller system. For the tests a balance was used, with which I
measured the force when running the inked disk on a paper (see fig. 6). An example of lines is shown
in fig. 7. The line width as a function of force is given by fig 8 for both types of disks.
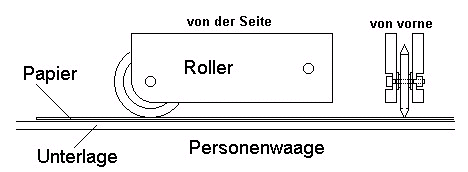
Fig. 6: Roller system used for printing on a paper using a balance (Personenwaage)
Ludwig Peetz Reconstruction of the Welte-Mignon T100 recording system technology p. 7
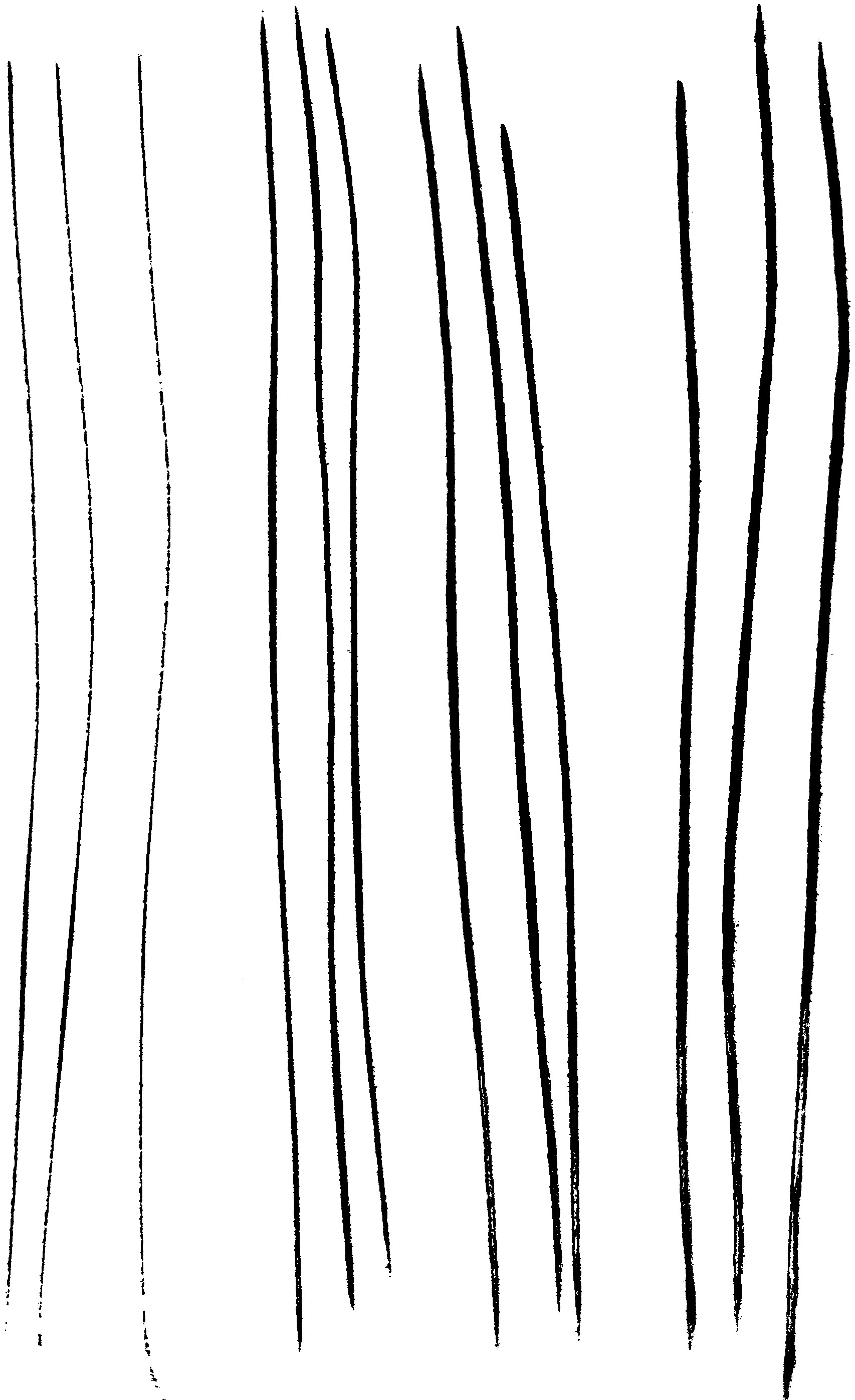
Fig. 7: Lines of different width using a roller with a sharpened disk at
around 0, 25, 50 and 75 N
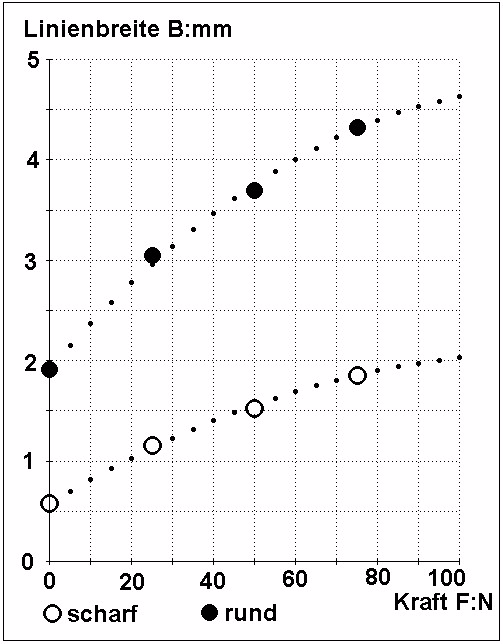
Fig. 8: Line width (Linienbreite B:mm) as a function of force (Kraft F:N) using a
sharpened disk (scharf) and an original round disk (rund)
The line width data (± standard deviation) of Fig. 8 are given in the following table:
Force F:N Line width B:mm
round disk sharpened disk
0 1,91 ± 0,18 0,58 ± 0,12
25 3,05 ± 0,14 1,15 ± 0,14
50 3,70 ± 0,18 1,53 ± 0,12
75 4,34 ± 0,24 1,85 ± 0,12
Ludwig Peetz Reconstruction of the Welte-Mignon T100 recording system technology p. 8
Both types of disks show a non-linear degressive behaviour of the line width as a function of the force.
The relative sensibility of the sharpened disk curve is higher as that of the original disk. Probably the
width at zero force will be lower if more regular industrially produced sharp disks are used. It is clear
that with softer disks there are higher gradients in the line width-force-curve.
7. Force / current relation of an electromagnet-iron plate combination
According to Coulomb's law the force F of an electromagnet pole exerted to an iron plate is
proportional to p²/r² where p = / 0 is the magnetic pole force, the magnetic flux, 0 = 4 10-7 the
magnetic field constant and r is the distance to the plate:
(10) F = a ² / r² (a > 0 constant)
As a first approximation p is proportional to the electrical current I through the electromagnet.
(11) F = b I² / r² (b > 0 constant)
But as known from magnetic hysteresis measurements, there are further phenomena which have to be
taken into account:
(a) The remaining magnetisation of the iron plate and the iron core of the electromagnet giving
an additional linear contribution to the force with respect to the current I.
(b) The magnetic saturation effect, leading to a mean current exponent lower than 2 in the force
(c) If in fig. 5 the current I rises the electromagnet will attract the iron plate and the distance r will be
reduced
Therefore the relationship between force F and current I may complexly depend e.g. on current level,
material composition and the form of the electromagnet and the plate.
Using the quadratic equation (11), the current I is proportional to the square root of the current I:
(12) (F:N)0,5 ~ I:A .
The corresponding relationship between Line width B and current I is given in Fig. 9, showing a
progressive non-linear behaviour.
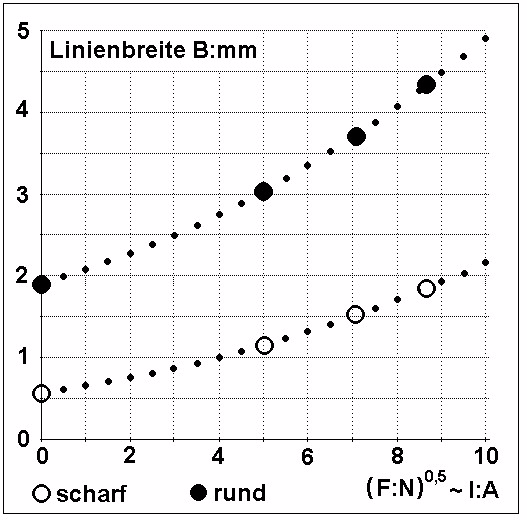
Fig: 9: Line width B:mm as a function of (F:N)0,5 which is proportional to the current I:A
Ludwig Peetz Reconstruction of the Welte-Mignon T100 recording system technology p. 9
8. How Piano Dynamics or the Loudness of a Tone has to be captured?
The principal question for the construction of a dynamic recording system is, how the dynamics of a
piano (or the loudness of a tone) is created. Is this done by the force that the pianist exert to the key or
by the velocity of the key?
There is a clear answer due to the working principle of the piano mechanics:
The only information needed is the momentary key velocity at one exactly defined key position, the
point where the hammer is leaving the lever (hammer leaving point HLP). The key velocity at this point
is strictly related to the hammer velocity hitting the string, and this velocity is related to the loudness of
the tone. What happens after the key has crossed the HLP is of no importance to the hammer
velocity. The hammer moves freely towards the string and its velocity cannot be influenced any more
by enhancing or reducing the force executed on the piano key.
Therefore as the only reliable measure of a tone's loudness the velocity v0 at the HLP must be
determined. This is the exact momentary velocity v0 = v(t0) given to the key by the pianist's finger at the
time t0, when the hammer leaves the lever to the string. At this moment the key position is at the HLP
h0 = h(t0) and the line width is B0 = B(t0).
An additional condition must be fulfilled to get a tone: v0 must exceed the well-defined minimum value
vmin that ensures that the hammer gets more kinetic energy than the potential energy needed to reach
the string.
9. Configuration of the Welte-Mignon recording system
It seems probably that at the Welte-Mignon recording grand piano the C-rods were connected directly
to the key, but running in a guiding tube. There is a spring to press the rod against the key, that it has
no degree of freedom. The rod just follows the key position directly (exactly spoken the projection of
the key movement in the tube direction; the key varies in angle but the guiding tube doesn't: it must be
fixed in a vertical position).
The felt has the function to slow down and stop the key (and the pianist's fingers) smoothly in a
progressive force / way curve; otherwise it would take too much time to damp the movement down
if heavy tones must be repeated very fast. The damping must begin after the hammer had left the lever
to the string (otherwise the pianist wouldn't control as well the tones). This can be shown by fig. 2:
The force-way function of the felt and the piano match each other, if it is assumed, that the 0-point of
the key position (with normal key position set to H = 10 mm) corresponds to a felt thickness of D = 4.94
mm. Since the HLP is at h0 = 1 mm it corresponds to a felt thickness of DHLP = 4,94 mm +1 mm = 5,94
mm, which is the practically the initial thickness of the felt (D = 6 mm).Therefore the felt and its non-linear force-way behaviour have no influence on the key velocity at the HLP and
higher positions. However below the HLP the key velocity is slowed down by the felt. Therefore it is
important to measure the key velocity in the felt-free zone above h0.
There is a next important point to consider:
In order to determinate whether a tone has been repeated or not it is necessary to measure, whether
the key was over the minimum height of the repeating mechanism (MHRM), which is at h2 = 3 mm, or
not.
If the key went over that point and then went down again, the tone was repeated and a new tone with
its corresponding new loudness occurs. If the key doesn't reach the MHRM then the tone was simply
hold (with no new loudness to determine apparently). To decide this, the MHRM must be included in
the measurement system. The best way is to set the initial contact of the rubber disk to the paper
exactly at the MHRM. In this configuration it can be decided easily whether a tone has been repeated
or not:
If the key was above the MHRM limit and went down again then the line shortly interrupts, which
shows that the tone was repeated. If the line didn't interrupt then the pianist had hold the tone (may be
with lower force as he had used at the HLP).
It follows that in a reliable dynamic measurement system using Hg/C-contacts there is a difference in
height between MHRM and HLP of about h = h2 - h0 = 2 mm, in which the key position must be
measured.
Ludwig Peetz Reconstruction of the Welte-Mignon T100 recording system technology p. 10
10. Determination of the exact value of v0 by a graphical tangent analysis
From the experimental data it seems clear that the function B(h) and its inverse function h(B) are non-linear. A graphical tangent analysis based on a differential calculus is a method known in the 19th
century /7/ with which it is possible to determine accurately the momentary velocity v0 under non-linear
conditions.
The non-linear functions B(h) and its inverse function h(B) can be determined experimentally by
measuring the line with at different key height positions:
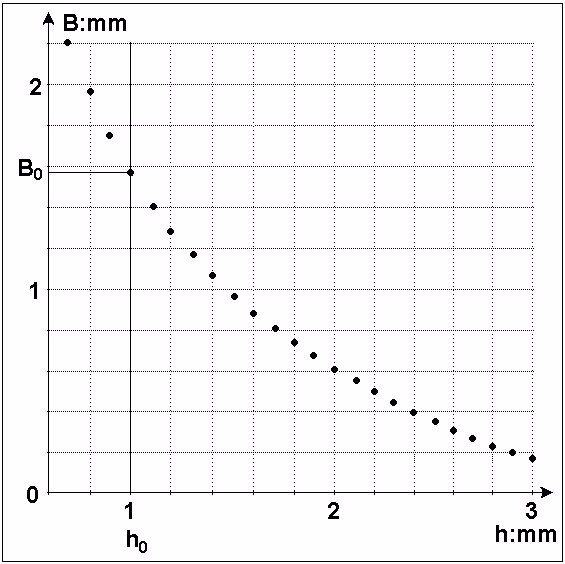
Fig. 10: Arbitrary non-linear line width function B(h) (example)
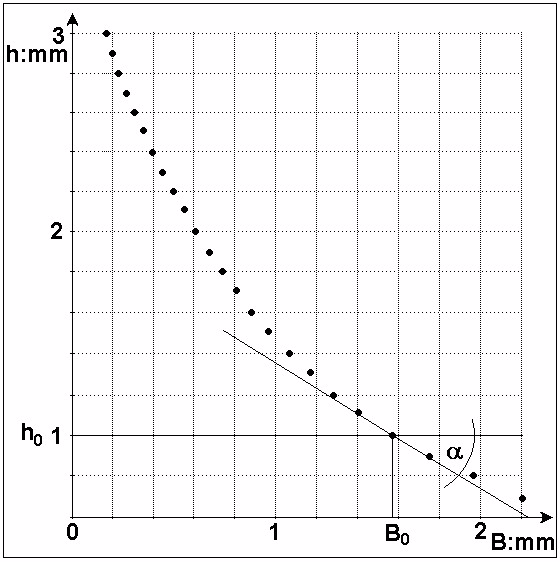
Fig. 11: Inverse function of fig. 10 h(B) with h'(B0) = tan
Ludwig Peetz Reconstruction of the Welte-Mignon T100 recording system technology p. 10
Fig. 10 and Fig. 11 show an arbitrary example of a non-linear line-width function B(h) and its inverse
function h(B) including the HLP-values h0 and B0 respectively. From fig. 11 the first derivation
(13) h'(B0) = tan()
can be determined by the drawing the tangent to the h(B) at B0 (see fig. 11). The angle as well as
tan() have negative values.
The dependence of the key position on time can be described by a chain of the functions h(B) and
B(t):
(14) h(t) = h(B(t)).
The momentary key velocity at t0 is given by the first derivation of the key position with respect to the
time
(15) v0 = v(t0) = - h'(t0)
The negative sign is chosen to define v0 as a positive value. Using the differentiation rule for chain
functions it follows
(16) v0 = - h'(t0) = - h'(B0 ) B'(t0) = - tan() B'(t0)
The time dependent line width B(t) is a chain function of the varying line-width B(L) printed to the length
L of the paper and the varying length L(t) of the printing position on the paper with time t:
(17) B(t) = B(L(t)).
The differentiation rule for chain functions leads to
(18) B'(t0) = B'(L0) L'(t0)
where
(19) L0 = L(t0)
is the paper length at the time t0, when the hammer leaves the lever and
(20) L'(t0) = vp
is the paper velocity vP at t0. Thus the momentary velocity v0 is given by
(21) v0 = - vP tan() B'(L0)
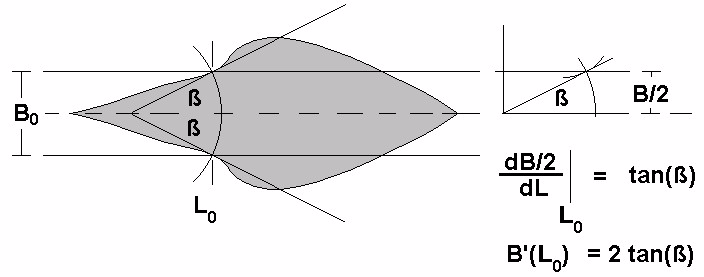
Fig. 12: Determination of L0 and B'(L0) from a printed line by a graphical analysis
Fig. 12 demonstrates how L0 and B'(L0) can be determined form a printed line by a graphical analysis.
The form of the line is very non-linear in an exaggerated manner. The non-linearity is due to any
acceleration or slowing-down effects exerted by the pianist to the key between MHRM and HLP (which
might be thought in this example as a very artificial play) and the non-linearity of the functions B(h) and
h(B).
L0 is given by the intersection of the line with two symmetrically centred parallel lines representing the
line-width B0 which corresponds to the HLP.
Ludwig Peetz Reconstruction of the Welte-Mignon T100 recording system technology p. 11
At the two intersection points at L0 tangents were drawn which form an angle 2ß. The value tan(ß)
corresponds to the first derivation of the half line-width B/2. Therefore it follows:
(22) B'(L0) = 2 tan(ß)
and the final result:
(23) v0 = - 2 vp tan() tan(ß).
Fig. 13 shows two arbitrary lines; in the case (a) there is no interruption of the line; therefore the key
has not been above the MHRM, only one note has been played; in the case (b) the interruption of the
line demonstrate that the key was over the MHRM, so that the note has been repeated with its own v0
determined by L0(2) and ß(2)
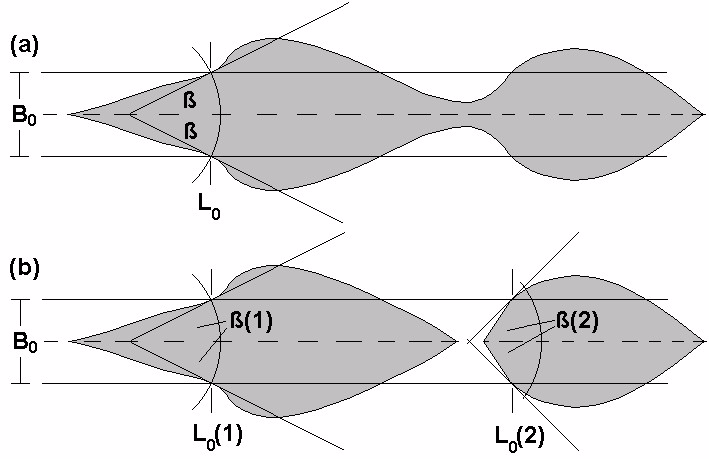
Fig. 13: (a) Only one note played without line interruption
(b) Two notes played with interruption
The question of the accuracy of this measurement system is a delicate one. Following Richard
Simonton the registration paper was a standard roll of 328 mm width, entirely blank with over 100 fine
lines. Such rolls are well-known /8/. There are even red perforated rolls which are equipped with lines
on the entire length. I possess an example of No. 401 Consolation No. 3 Fr. Liszt, played by Ernst von
Dohnanyi recorded the 13.IX.05, with 102 lines on the entire length. Since the separation of the lines is
3.2 mm the maximum line width is limited to the order of 3 mm.
For a high accuracy a measuring microscope could be used. End of the 19th century the accuracy of
such equipment was up to 0,001 mm = 1m using glass plates with diamond-engraved grids /9/. Even
mechanical screw micrometers reached that accuracy /10/, /11/. Furthermore it should be noted that
the accuracy of angle measurements by standard sextants with nonius scale was 20" = 1/180° /12/.
The basic accuracy can be enhanced by taking mean values of many measurements. In terms of
reproducibility a standard deviation of the mean values of ß of than lower than 20" could be reached.
It's only a question of statistics, the more measurements the better is the accuracy. However there is a
bigger problem: the absolute accuracy. The piano mechanism and the Hg/C-contacts and the disks
registration system must be adjusted for each key in the same way. It can be assumed that an absolute
accuracy of a few percent could be reached at best. In this case a sophisticated measuring method
which takes a long time for each note is only of theoretical interest.
A more practical easy and fast evaluation system can be constructed using a glass goniometer with 5
diamond-engraved parallel lines with distance B0/2 under a magnifying glass:
Ludwig Peetz Reconstruction of the Welte-Mignon T100 recording system technology p. 12
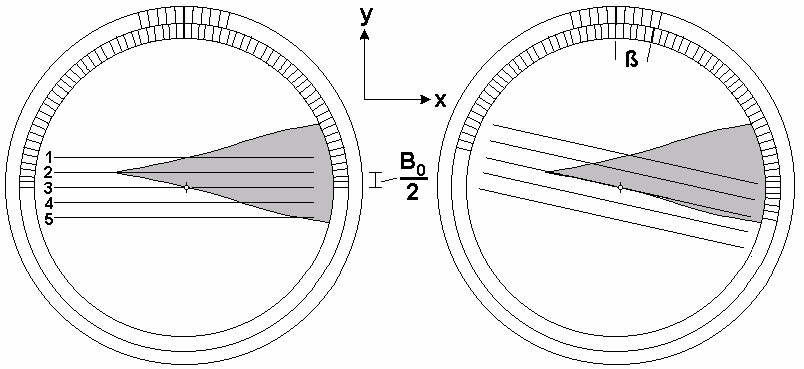
Fig. 14: Goniometer used under a magnifying glass for easy and fast determination of ß
The goniometer is connected to a paper rolling device were the paper position in x-direction (Length L)
is measured separately. The goniometer itself can be displaced in y-direction, so that its line 2 is set
parallel to the base line of the regarded note. Then the paper is displaced in x-direction until the lines 1
and 3 fit the line width. The goniometer has to be turned until the line 3 is the tangent of the curve at
the rotational axe. The angle ß can be read accurately by a nonius scale. The opposite value of ß is
measured in the same manner using the lines 3 and 5 with the base line of the note centred to line 4.
Finally there will be a list of all notes of a registered music piece with its two ß values from which a
mean value is taken. By equation (23) the momentary key velocity v0 at HLP can be calculated.
Since the times of Newton it is known that the momentary velocity is defined by the differentiation of
the way with respect to time. Therefore a correct evaluation must involve a differentiation process. The
easiest way to differentiate a curve in the 19th century was a graphical tangent analysis. Another way to
get an even better (more objective) approximation of h'(B0) would involve a Taylor development of h(B)
around B0
(24) h(B) = H(B0) + h'(B0) (B- B0) + h''(B0) (B- B0)² / 2 + ... + h(n)(B0) (B- B0)n / n!
to the desired degree n of non-linearity and a least squares fit according to Gauss using a huge
number of data points in the vicinity of B0. This leads to the best approximation value of h'(B0) = tan()
with respect to the data set but implies a considerable mathematical calculus effort. Since h'(B0) must
be determined only one time this effort may be justified. A similar evaluation is possible in the case of
B'(L0) = 2 tan(ß) but for each note the calculus effort is to high in a practical application.
There are many other ways to get more or less reliable approximated values of v0. The simplest way is
a two point calculation of the mean velocity <v0>. This method was e.g. used in Nyström's Melograph
in 1911 /13/ and in the AMPICO B- spark-chronograph system developed in 1929 /14/. It has to be
noted that the mean velocity calculation neglects all acceleration and slowing down effects exerted by
the pianist on the key.
In the Welte-Mignon-Hg/C-elastic disk recording system the mean velocity between the MHRM with
height h2 and the HLP with height h0 can be determined by measuring the length of the line from its
beginning at the paper length L2 to L0 at HLP. With the definitions
(25) h = h0 - h2 (negative value)
(26) L = L0 - L2 (positive value)
and the calculation of the time difference
(27) t = L / vP
it follows:
(25) <v0> = - h / t = - vP h / L
Ludwig Peetz Reconstruction of the Welte-Mignon T100 recording system technology p. 13
Any other pair of points i and j near the HLP with heights hi and hj can be used in the same manner.
This evaluation takes into account the non-linearity of the B(h) curve but not that of the pianist's play.
Additional points can be introduced to get information on the pianist's acceleration (or slowing down)
effects; e.g. by 3 points the mean acceleration <a0> can be taken into account. As well it is possible to
use an empirical correlation between maximum line width Bmax, <v0> and <a0> to improve accuracy.
However the graphical tangent method clearly is the best evaluation method because it delivers directly
the momentary velocity v0.
CREDITS & REFERENCES USED IN DR. PEETZ'S ARTICLE
/1/ A. Binet, J. Courtier, Recherches Graphiques sur la Musique, in: L'Année psychologique, 2e année - 1895, p. 201-222, Alcan, Paris (1896).
/2/ Johann Friedrich Unger: Entwurf einer Maschine, wodurch alles was auf dem Clavier gespielt wird, sich von selbst in Noten setzt (1745, 1752, 1774); article by Jürgen Hocker in DMM 26, Sept. 82, p. 14-16 and DMM 27, March 1983, p. 21
/3/ Richard Simonton jr., MMD 2000.01.28®13
/4/ Ben M. Hall, „How is it possible? - The Welte Technique explained -" in Q. David Bowers; Encyclopedia of Automatic Musical Instruments, Vestal Press, Vestal, New York 1972 p. 327
/5/ Kurt Binninger, Die Welte-Philharmonie-Orgel,
/6/ Information by Hans. W. Schmitz, Stuttgart (he drawed the original of fig. 5 in Binninger's article)
/7/ Brockhaus Konversations-Lexikon 17. Auflage 1894 no. 5 p. 298-299 (Differentialrechnung)
/8/ There are several examples in the Edwin Welte heritage used for the transformation from T100 to T98 system (see Gerhard Dangel-Reese: MMD 2000.02.09®11)
/9/ Brockhaus Konversations-Lexikon 17. Auflage 1894 no. 11 p. 871 (Mikrometer)
/10/ Brockhaus Konversations-Lexikon 17. Auflage 1894 no. 11 p. 871-872 (Mikrometerschraube)
/11/ Brockhaus Konversations-Lexikon 17. Auflage 1894 no. 5 p. 299 (Differentialschraube)
/12/ Brockhaus Konversations-Lexikon 17. Auflage 1895 no. 14 p. 896-897 (Sextant)
/13/ Peter Hagmann, Das Welte-Mignon-Klavier, die Welte-Philharmonie-Orgel und die Anfänge der Reproduktion von Musik, Verlag Peter Lang , Bern, Frankfurt, New York 1984; p. 69-71
Note: the full text can be obtained by http://freidok.uni-freiburg.de/volltexte/608/ (File: hagmann.pdf 2082 KB); see also: Gerhard Dangel, „Das Welte-Mignon-Klavier" by Peter Hagmann, MMD 2003.01.09 ® 03 und Robbie Rhodes, Contents of „Das Welte-Mignon-Klavier" by Peter Hagmann, MMD 2003.01.09 ® 04
/14/ Peter Hagmann, Das Welte-Mignon-Klavier, die Welte-Philharmonie-Orgel und die Anfänge der Reproduktion von Musik, Verlag Peter Lang , Bern, Frankfurt, New York 1984; p. 71-76.

